k近傍法(k-NN)の理解と簡単なPython実装

こんにちは、@Yoshimiです。

機械学習には多くのアルゴリズムがありますが、「Pythonで始める機械学習」のなかで、最も単純な学習アルゴリズムと言われているk近傍法(k-NearistNeighbor)の実装にチャレンジしましょう。k近傍法(k-NearistNeighbor)は分類問題などに使いますが、とても似た名前にk平均法(k-means)があるりますが、k-meansは教師なし学習でクラスタリングに使います。

1 k近傍法(k-NN)とは？
- 1.1 ユークリッド距離
- 1.2 マンハッタン距離
2 Pythonで実装してみよう
- 2.1 実際のpythonコード
- 2.2 canserデータセットで確認する
3 フルスクラッチで実装してみる
4 最後に

k近傍法(k-NN)とは？

分類したいデータと既存のデータとの距離を計算し、距離が近いk点のデータの多数決でクラスを決定します。
例えば、「k=3のときは『?の緑◯点』から距離の近い3点をデータの仲間である」とします。

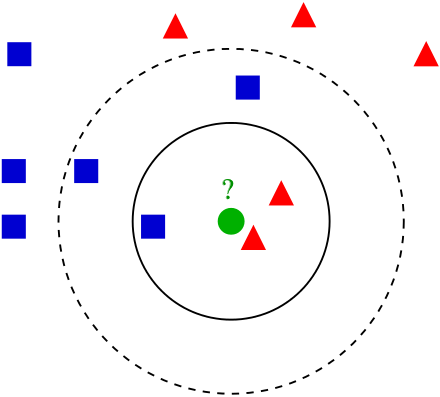
k近傍法の例。標本（緑の丸）は、第一のクラス（青の四角）と第二のクラス（赤の三角）のいずれかに分類される。k = 3 なら、内側の円内にあるオブジェクトが近傍となるので、第二のクラスに分類される（赤の三角の方が多い）。しかし、k = 5 なら、それが逆転する。
引用：wikipedia

k近傍法(k-NN)の使う場面は分類タスクで活躍できます。

顧客の購買行動予測
クレジットカードの不正利用検知
キノコの種類を予測する

ざっくりとメリットデメリットは以下のようなことがいえます。

メリット

精度はそんなに悪くない（特筆して良いかというとそうでもない）
直感的でブラックボックス的な予測ではない

デメリット

毎回学習データ毎に距離の計算を行うので処理速度が遅い（計算量が多い）
入力データの次元数が多くなると精度が出ない
ノイズに弱い

冒頭で、「分類したいデータと既存のデータとの距離を計算・・・」と説明しましたが、「距離」とか「次元数」とか何を言っているのかわからない・・・という方のためにも私のわかる範囲でしっかりお伝えしますので安心して下さい。距離の計算には一般的には「ユーグリッド距離」が使われますが、他にも「マンハッタン距離」「チェビシェフ距離」があります。

ユークリッド距離

2点間の直線距離のことです。公式はこんな感じです。
$$d(A,B)=\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}$$

マンハッタン距離

碁盤の目のように区画された道しか通れない状況で測るような距離です。
$$d(A,B)=|a_1-b_1|+|a_2-b_2|$$

ユークリッド距離とマンハッタン距離を図で表すと下図のようになります。
具体的にみてみましょう。

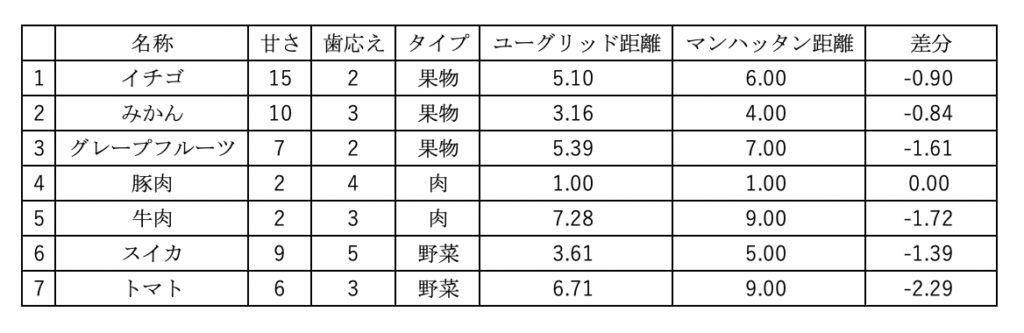
計算してみてもユーグリッド距離の方が2点間の距離が近いです。そのため、一般的にユーグリッド距離が使われています。しかし、マンハッタン距離でないと計算できないという場合もあるようです。それは平行移動しかできない時とのこと。このブログを読んでいただいているレベルであれば、まずはユーグリッド距離とマンハッタン距離（他にチェビシェフ距離）があることと、距離の計算方式を知っておけば十分だと思います。

Pythonで実装してみよう

書籍「Pythonで始める自然言語処理」を参考に知識アップしていきます。もちろんこの１冊を読めば理解は深まると思いますが、初心者には若干難しめの内容になっていると思うので、噛み砕いていきます。

fogeデータセットで確認していきます。

from IPython.display import set_matplotlib_formats, display
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import mglearn
from cycler import cycler

X, y = mglearn.datasets.make_forge()
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.legend(["Class 0", "Class 1"], loc=4)
plt.xlabel("First feature")
plt.ylabel("Second feature")
plt.show()
print("X.shape: {}".format(X.shape))

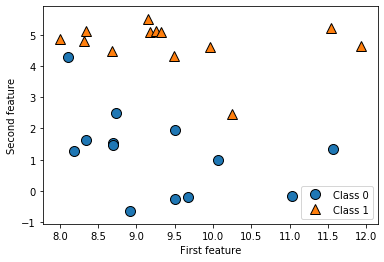上図でも確認取れるように2つの特徴量を持つ26のデータポイントで構成されています。

n_neighbors=1のようにk=1とすることで訓練データのうち最も近い距離のテストデータを選びます。

mglearn.plots.plot_knn_classification(n_neighbors=1)

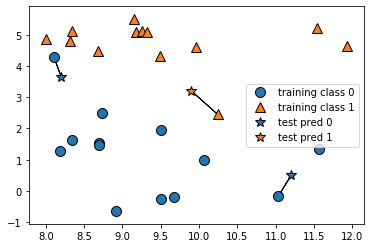「あれ？K=●部分で、複数選択できるけど、最短距離がわかればk=1でよくない？」と思いますよね。私も初めはそう思いました。しかし、精度に関わってくるというのがあります。複数Kを設定する（1つ以上の近傍点を考慮する）場合は、投票でラベルを決めます。より精度が高い結果になる可能性があるということです。

下図はn_neighbors=3としています。

mglearn.plots.plot_knn_classification(n_neighbors=3)

実際のpythonコード

上からの流れで実際のコードを確認していきます。

from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split

X, y = mglearn.datasets.make_forge()

# train_test_splitで分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

# インスタンスの生成、3つの近傍点で投票を行う
clf = KNeighborsClassifier(n_neighbors=3)

# 学習する
clf.fit(X_train, y_train)

n_neighbors=3だけ設定しましたが、他はデフォルトです。

KNeighborsClassifier(algorithm=’auto’, leaf_size=30, metric=’minkowski’,
metric_params=None, n_jobs=None, n_neighbors=3, p=2,
weights=’uniform’)

print("Test set predictions: {}".format(clf.predict(X_test)))
print("Test set accuracy: {:.2f}".format(clf.score(X_test, y_test)))

Test set predictions: [1 0 1 0 1 0 0] Test set accuracy: 0.86

およそ86%の精度であることがわかりました。

どんな分類がされたのか可視化してみます。
決定境界をみてみます。

# figsize: インチ数
fig, axes = plt.subplots(1, 3, figsize=(10, 3))

for n_neighbors, ax in zip([1, 3, 9], axes):
    clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
    # plot_2d_separator: 色で二分割
    mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4)
    # discrete_scatter: 要素を分布
    mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
    ax.set_title("{} neighbor(s)".format(n_neighbors))
    ax.set_xlabel("feature 0")
    ax.set_ylabel("feature 1")
axes[0].legend(loc=3)
plt.show()

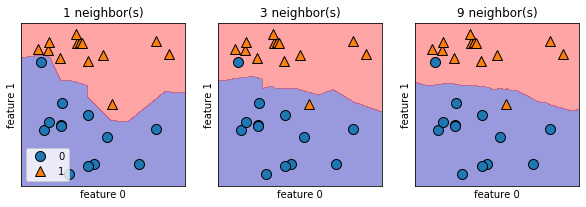1つの近傍点と9つの近傍点では色分けに差があります。近傍点が少なくなれば複雑どの高いモデルに対し、近傍点が多ければ複雑度の低いモデルに対応することがわかりました。

canserデータセットで確認する

canserデータセットで汎用性があるか確認してみましょう。

from sklearn.datasets import load_breast_cancer

cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
    cancer.data, cancer.target, stratify=cancer.target, random_state=66)

training_accuracy = []
test_accuracy = []

neighbors_settings = range(1, 11)

for n_neighbors in neighbors_settings:
    clf = KNeighborsClassifier(n_neighbors=n_neighbors)
    clf.fit(X_train, y_train)
    training_accuracy.append(clf.score(X_train, y_train))
    test_accuracy.append(clf.score(X_test, y_test))

plt.plot(neighbors_settings, training_accuracy, label="training accuracy")
plt.plot(neighbors_settings, test_accuracy, label="test accuracy")
plt.ylabel("Accuracy")
plt.xlabel("n_neighbors")
plt.show()

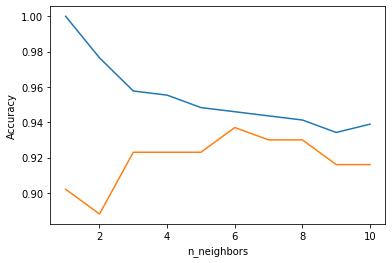
上図では、近傍点が2つ（k=2）でもAccuracyは88%ほどあり比較的精度が高いといえます。しかし、kが増えていくことで精度が高くなったり、低くなったりもしており、k=10ではk=6からの最低の精度です。この図を見る限りではk=6が最高の精度になっていることがわかります。