Python

決定木(Decision Tree)のアルゴリズムを少し覗いてみる

こんにちは、@Yoshimiです。

機械学習でなんとく決定木(Decision Tree)を使っていました。複数のアルゴリズムで検証するようになり、改めてどんなアルゴリズムなのだろうかと気になったので、調べ直しました。調べれば調べるほど、当たり前ですが非常に難解です。研究者のブログでは読まれることもないというのとボロが出るでの概要をまとめておきます。（長文になりました。）

決定木(Decision Tree)

決定木(Decision Tree)とは、「段階的にデータを分割していき、木のような（ツリー状の）分析結果を出力する」。もっと砕いたイメージで表現するのであれば、「条件による分岐を設け、根から辿り、最も条件に合致する方に分かれていく」アルゴリズムです。（ですが、正確には「決定木」とは特定のアルゴリズムを表す用語ではないです。）

例えば、「ジョギングをするか」の質問で、「YESの場合、天気が晴れの場合、さらにYESの場合、湿度は70%であればジョギングをするか？さらにYESの場合・・・」と条件によって枝分かれしていきます。

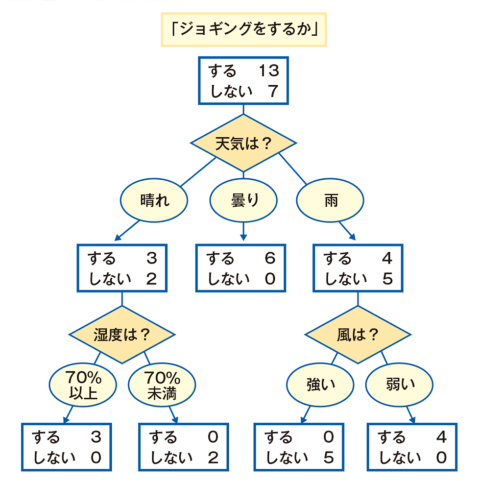
見た目が「木」なのでそのまま「木」とよばれます。実際に計算を行う青四角の部分を「ノード」、計算結果後に進む経路（この場合は矢印→）を「エッジ」と呼ぶようです。

もちろん「決定木」にもメリット・デメリットがあります。

メリット

  • モデルの可読性が高い（どういう基準で分けたかの可読性が高い）
  • 様々な尺度のデータをそのまま扱える（様々な設定が可能）
  • バイアスが低い（結果から予測した値と実際の正解の誤差が小さい）
  • データの前処理（スケーリング等）にとのなう負担が少ない
  • 「分類」にも「回帰」にも利用可能

デメリット

  • 高い分類性能ではない
  • 過学習を起こしやすい
  • バリアンス（ズレ）が大きい

メリットで「分類」にも「回帰」にも利用可能と説明しておりますが、実は「分類木」と「回帰木」と種類があり、この二つが組み合わさったものが「決定木」です。

分類木

下図のように、日々の温度と湿度の関係を表した散布図があるとします。
赤●点：A君 / 青●点：B君
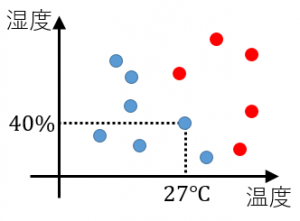赤●点はA君が暑いと感じた日、青●点はB君が暑いと感じた点です。A君とB君では感じ方が違うのがわかります。

A君とB君での感じ方の違いを表現したツリーです。
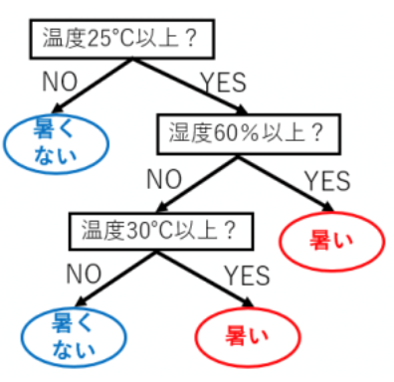分類のルールをツリーで表した図が分類木といいます。

回帰木

下図のように、日々の温度と湿度のデータ、および、その日にA君が飲んだ水の量のデータがあります。
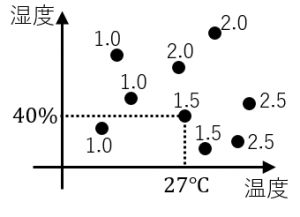1つの●点が1日を表します。数字は飲んだ水の量です。

この図から温度と湿度がわかる時の水の量はどれくらいか？を表した図が下のツリーになります。
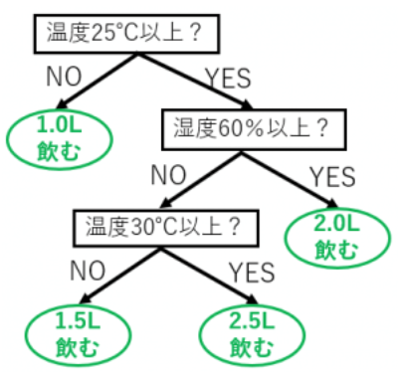ある数値（連続値）の推定のルールをツリーで表現したものを回帰木と言います。

（専門家のように紹介しましたが、こちらのページを参考にさせてもらっています。）

決定木の学習

決定木の手法にはCART（Classification and Regression Tree）、CHAID、C4.5(C5.0)がよく使用されるあるアルゴリズムです。

そして、決定木の各ノードがうまく条件分岐を作成できるているか否の指標として不純度(impurity)があります。そして、その不純度(impurity)を考える上での指標でエントロピー（entropy）とGini係数があります。

複雑ですね。

CART（Classification and Regression Tree）

大枠は下記３点を抑えておけば大丈夫じゃないでしょうか。

  • 分岐の指標には不純度を表すGINI係数を基準に分割
  • GINI係数は0~1の間で値をとり、0に近いほど平等（純粋）
  • ノードを分割することで、不純物が減少していく（純度がます）

分割条件の良し悪しを判断するために、分割前後の不純度の変化を次式で定義します。
$$E(t) = 1-\sum_{i=1}^{K}P^2(C_i|t)$$

CHAID

  • 分岐の指標にはカイ2乗統計量を基準に分割
  • 多分岐が可能
  • 過学習する前に学習を止める
  • 目的変数が量的変数の場合は、同じく統計的検定の手法であるF検定を用いることがある

C5.0

  • 分岐の指標にはエントロピーに基づくゲイン比という基準で分割
  • 情報量：確率pで起こる事象の情報量じゃ-log２pで定義される
  • log2pの絶対値が大きい=情報量が多い
  • エントロピーが低いほどノードの純度は高い

エントロピーの数式
$$H(X) = – \sum^n_{i=1}p_i \log_2{p_i}$$

難しいですね・・・

まとまった資料があるのでご確認ください。

引用：決定木の概要

決定木を確認してみる

機械学習チュートリアル的存在irisのデータセットを使って、決定木を確認してみます。sklearn0.21にてsklearn.tree.plot_treeが実装されており、簡単に決定木を表示させることが可能です。

基本的なモジュールを読み込みます。

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
%matplotlib inline

irisというモデルの箱を作り、学習させます。DecisionTreeClassifier()が決定木になります。

iris = load_iris()
model = DecisionTreeClassifier()
model.fit(iris.data, iris.target)

決定木を確認します。

fig = plt.figure(figsize=(15, 8))
ax = fig.add_subplot()
plot_tree(model, feature_names=iris.feature_names, ax=ax, class_names=iris.target_names, filled=True);

下図のような決定木は出力できましたか？条件からTrue or Falseで分岐していきます。

決定木のイメージはつきましたか？

sklearn.tree.DecisionTreeClassifier クラスの書式です。各パラメータの変更に役立ててください。

DecisionTreeClassifier(criterion='gini',
                                  splitter='best',
                                  max_depth=3,
                                  min_samples_split=3,
                                  min_samples_leaf=1,
                                  min_weight_fraction_leaf=0.0,
                                  max_features=4,
                                  random_state=None,
                                  max_leaf_nodes=8,
                                  min_impurity_split=1e-07,
                                  class_weight='balanced',
                                  presort=False)

人力ですべてのパラメータで最適なパラメータを探すには不可能に近いのでグリッドサーチなどで探索することをお勧めします。

パラメータ名 パラメータの意味
criterion 分割する際に利用する品質。ジニ係数を利用する “gini” と情報量を示す “entropy” のいずれかを指定。(省略時は “gini”)
splitter 各ノードにおいて分割を行う方法を選択。”best” (最適) または “random” (ランダム最適) を選択。(省略時は “best”)
max_features 最適な分割を探索する際に用いる特徴数の最大値。
max_depth 作成する決定木の深さの最大値。 (省略時は None)
min_samples_split サンプルを枝に分割する数の際の枝の数の最小値。 (省略時は 2)
min_samples_leaf 1 つのサンプルが属する葉の数の最小値。 (省略時は 1)
min_weight_fraction_leaf 1 つの葉に属する必要のあるサンプルの割合の最小値。 (省略時は 0.0)
max_leaf_nodes 作成する葉の数の最大値。数値を指定した場合は、max_depth が無視されます。 (省略時は None)
class_weight 各説明変数に対する重み。 (省略時は None)
random_state 乱数のシードを指定。指定しない場合は、 np.random を利用します。 (省略時は None)
presort 高速化の目的で事前に入力データのソートを行うかどうか。 (省略時は False)

最後に

機械学習を学ぶ時、まず決定木から学習していくことが多いと思います。決定木の発展系であるランダムフォレストやXGBoostなどを理解していくためには、根幹となる決定木の理解がある程度あった方が良いです。また、発展として、決定木＋アンサンブル学習などもあるので、この際時間をかけてお勉強しちゃいましょう。決定木の人気さも資料で上がっているので確認してみてください。

これでマスターしたわけでもないので、まだまだこれからも勉強あるのみです。

参考：
決定木
決定木分析（ディシジョン・ツリー）
決定木の学習
決定木による学習
決定木学習
scikit-learn で決定木分析 (CART法)


なりたい自分になれる
スキルアップならUdemy

私も利用し、高収入エンジニアになったのよ。未経験から機械学習、データサイエンティスト、アプリ開発エンジニアを目指せるコンテンツが多数あります。優秀な講師が多数！割引を利用すれば1,200円〜から動画購入可能です。！

高収入エンジニアになる >>





ABOUTこの記事をかいた人

大学卒業して、キラキラしていたのでIT業界にはいりましたが、中身はブラックでした！！だから、投資技術を磨いて早くリタイヤしたいです。株価、Python、機械学習をもうもう勉強中です。経済的自由を手に入れて農家やりたい！

RECOMMENDこちらの記事も人気です。