何か商品をつくり販売、リリースしたものの、その後、本当のところどんなユーザーが購入しているのか気になりませんか?プロダクトを企画する際、ペルソナ、ターゲティングを行うことは当たり前ですが、そのプロダクトテーマにそったユーザーが購入しているのかを把握することで次の戦略につながります。
そんな課題を解決してくれる一つとしてロジスティック回帰分析があります。
ロジスティック回帰って何?
ロジスティック回帰とは、様々な要因から、ある事象が発生する確率を予測する式を作ることです。例えば、タイタニック号の乗船客の生存確率や商品の購入確率を予測したいときに用いられます。
似た言葉で重回帰分析というのがありますが、大きく違うのは目的変数の種類です。
- 重回帰分析:目的変数が連続値
- ロジスティック回帰分析:目的変数が二値
簡単に説明させてもらうと二値とはまさに、二つの値であり、YES/NOです。
例えば、
- スタッフが退職する / しない
- 商品が売れる / 売れない
- ローン返済ができる / できない
という感じです。プログラム的には0,1で判断するイメージです。
では、重回帰分析はその逆ですね。YES / NOで回答することがない分析です。
例えば、住宅の家賃 / 弁当の値段 / 株価などです。家賃であれば80,600円、弁当520円、株価10,000円と変動する値です。詳しくは別の機会に・・・
さて、ロジスティック回帰分析では、YES/NOの確率を知りたいわけです。となると答え(目的変数)は0~1の間に収まって欲しいわけです。つまり、重複説明しますがロジスティック回帰分析では、目的変数に指定した事象が発生する確率pを予測する式を作成します。
ロジスティック回帰分析ではシグモイド関数を利用します。
シグモイド曲線は入力した値を0から1の間に収めてくれる関数の1つです。その曲線を作る関数のことです。
$$f(x)=\frac{1}{1+e^{-ax}}$$
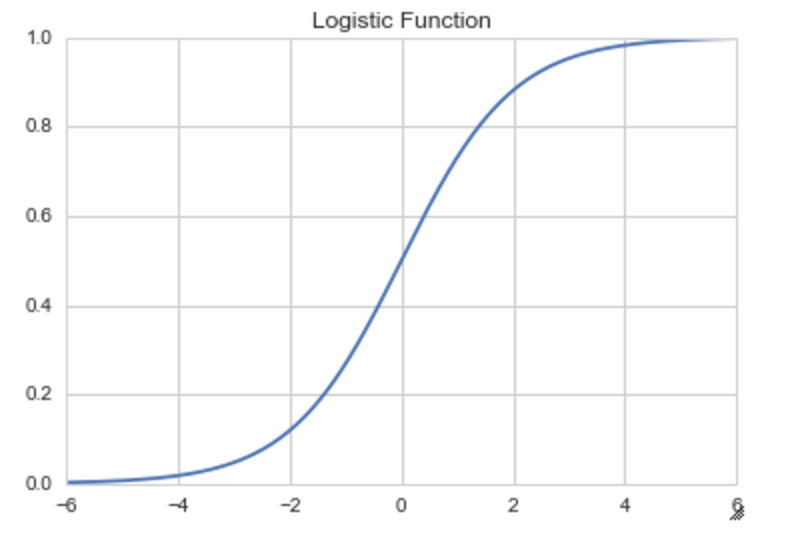 ちなみにPythonでは以下のような形になっています。
ちなみにPythonでは以下のような形になっています。
# ライブラリのimport
import numpy as np
import matplotlib.pyplot as plt
# ロジスティック関数
def logistic_function(x):
return 1/ (1+ np.exp(-x))
# プロットの作成
x = np.linspace(-10,10,1000)
plt.plot(x, logistic_function(x))
plt.title("logistic function")
plt.xlabel("x")
plt.ylabel("y")
線形回帰とは?
線形回帰というのがあります。線形回帰とは散らばってるデータに対して、散らばり方のルールを直線と仮定して、どんな直線なのかを調べることです。
例えば、下記のような身長と体重のデータがあったとします。
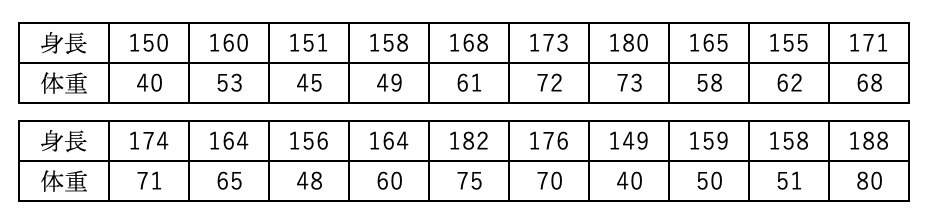 これを線形回帰を用いると下記のように予測グラフを作成することができます。
これを線形回帰を用いると下記のように予測グラフを作成することができます。
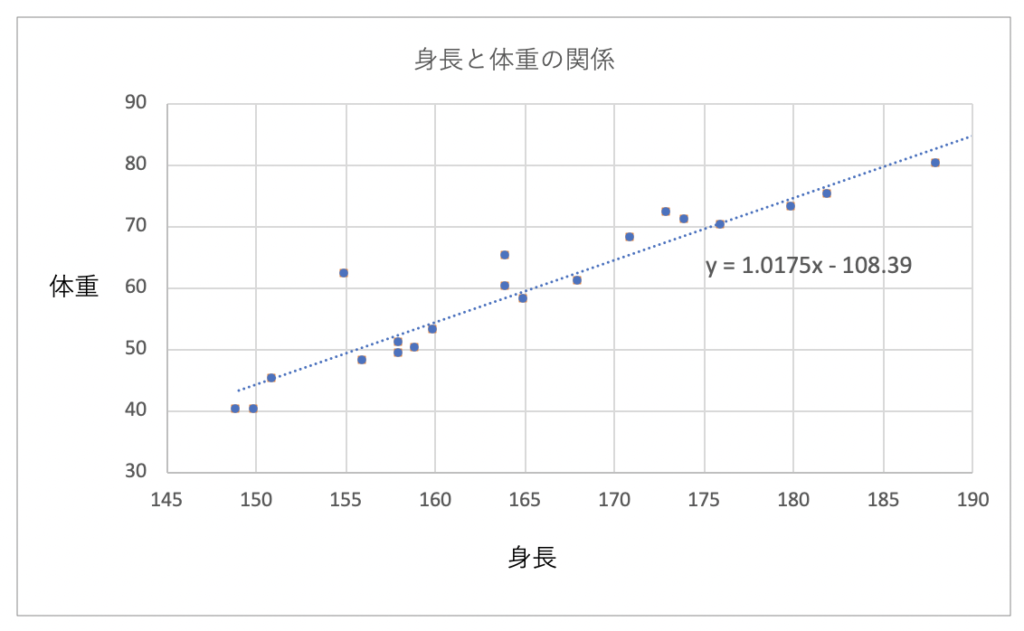 このグラフでは、「y = 1.0175x – 108.39」のx部分に身長の値を代入すると体重の値が予測できるというモデルです。
このグラフでは、「y = 1.0175x – 108.39」のx部分に身長の値を代入すると体重の値が予測できるというモデルです。
しかし、ここで考えなくてはいけないのが、元あるデータが直線状にないということです。グラフを見ていただいてわかる通り、点は直線の上にありません。直線と点の間には距離があります。この距離を誤差をいいます。この直線とそれぞれの点の距離の和(誤差の和)が最小になる直線を導き出す方法を、最小2乗法といいます。
詳細説明は脱線してしまうので割愛しますが、このような回帰もありますので参考までに。
ロジスティク回帰モデル
Pythonでロジスティック回帰モデルの作成を行ってます。
今回は、Pythonでロジスティック回帰分析を勉強するには、チュートリアル的存在のdatasetsで進めていきます。
sciket-laernを使っていきます。sciket-laernはPython の機械学習のモジュールです。
以下のような特徴があります。
- NumPy, SciPy や Matplotlib と互換性を持つように開発されています。
- オープンソースで公開されており、無料利用・商用利用も可能です。(BSDライセンス)
- 回帰、分類器、次元圧縮やクラスタリング、データの前処理をはじめとする、機械学習のアルゴリズムを幅広く実装されている
ですので、機械学習といえばsciket-laernといっても過言ではない必須モジュールです。
sciket-laernにある乳がんデータセットを使用していきます。
がん検診患者の診断情報30個を特徴量に、対象患者がガンであるか否かを教師ラベルとして持つデータです。
では早速進めていきます。
ライブラリのimportをします。
import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt from sklearn import datasets from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression as LR
今回のモジュール説明詳細をはgithubに上げておきますので確認してください。
「from sklearn import datasets」でデータセットを読み込みます。ちなみにsklearnのデータセットには種類があるので興味があれば、こちらも確認してみてください。
データセットを読み込みます。
cancer = datasets.load_breast_cancer() df = pd.DataFrame(cancer.data, columns= cancer.feature_names) df["label"] = cancer.target df.head()
データを確認してみるとこんな感じです。
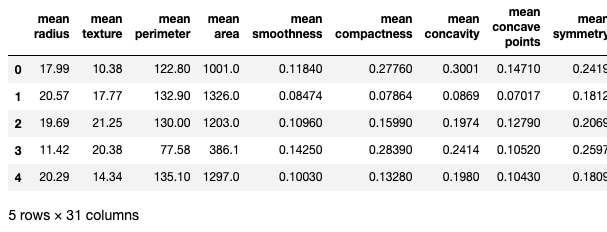 31 columnsとあるので、説明変数があることに注目です。
31 columnsとあるので、説明変数があることに注目です。
今回、求める説明変数はlabelです。(列が長すぎてキャプチャー外になってしまいました。)
df['label'].value_counts()
0 212
Name: label, dtype: int64
1(良性)が357、0(悪性)が212とあります。
Cancerデータを訓練データとテストデータ(20%)に分割します。
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, test_size=0.2, random_state=123)
分割したデータを確認してみます。
print('train : ', len(X_train))
print('test :', len(X_test))
print('trainの割合 :', len(X_train) / len(df))
test : 114
trainの割合 : 0.7996485
train dataに455、test dataに114、割合として、trainに80%なのでtestに20%ということになっています。
モデルの学習と評価を行います。
- モデルの作成
- モデルの学習
という流れです。
# モデルのインスタンス(箱)を作成 clf = LR() # fitメゾットで学習 clf.fit(X_train, y_train)
C=1.0, class_weight=None, dual=False, fit_intercept=True,intercept_scaling=1, l1_ratio=None, max_iter=100,multi_class=’auto’, n_jobs=None, penalty=’l2′,random_state=None, solver=’lbfgs’, tol=0.0001, verbose=0,warm_start=False
)
これで学習ができました。
表示されているパラメータを変更することで細かい学習設定が可能です。
このclf()のpredictメソッドにテストデータを渡すと、そのテストデータに対する予測ラベルが出てきます。
clf.predict(X_test)
0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1,
1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0,
0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0,
1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1,
0, 0, 0, 0])
学習の結果の評価を確認するにはscoreメソッドを使います。
教師データのスコアを算出します。
clf.score(X_train, y_train)
高いのは当然ですね。
では、test dataでスコアをみてみましょう。
clf.score(X_test, y_test)
高い数値が出ました。
これでロジスティク回帰による解析は終了です。
最後に
チュートリアル的なデータを利用しての検証ですので、高い精度が出ております。また、二値分類のアルゴリズムは他にもあります。解析内容によって、高い精度が出るもの、出ないものもあるので様々なアルゴリズムを試してみると良いと思います。
そして、今回はデータの値のみでロジスティック回帰分析を行いました。説明変数もそのままです。説明変数の各関係性や目的変数に対しての相関関係、擬似相関もあるかもしれません。特徴量が少ないという時もあるでしょう。そのようなことを見つけるために可視化(matplotlib利用)でヒントを見つける作業も必要になってきます。



