混同行列・python・sckit-learn・機械学習を理解したい！ための記事

機械学習の分類問題の検証で出てくる混同行列 (Confusion matrix)があります。サンプルコードはたくさんあるのだけど、そもそものTP、TN、FP、FNの意味をいまだに理解不足なので、自分なりにまとめてみました。

混同行列(Confusion Matrix)

常日頃、「分類」という作業が行われています。スパムメールの分類、融資を返金するかしない、病気なのかそうでないか・・・

機械学習の分類結果の精度を検証するために、混同行列(Confusion matrix)が主に使われています。混同行列をつかうことにより、正しく選別された件数、および間違って選別された数を比較できます。比較結果を元に機械学習で作成されたモデルを検証します。

例えば、融資の返済する・しないの課題があった場合、

• 横方向に「返済する、返済しないとモデルが識別した件数」
• 縦方向に「実際に融資を返済する（した）・返済しない（しなかった）

となります。
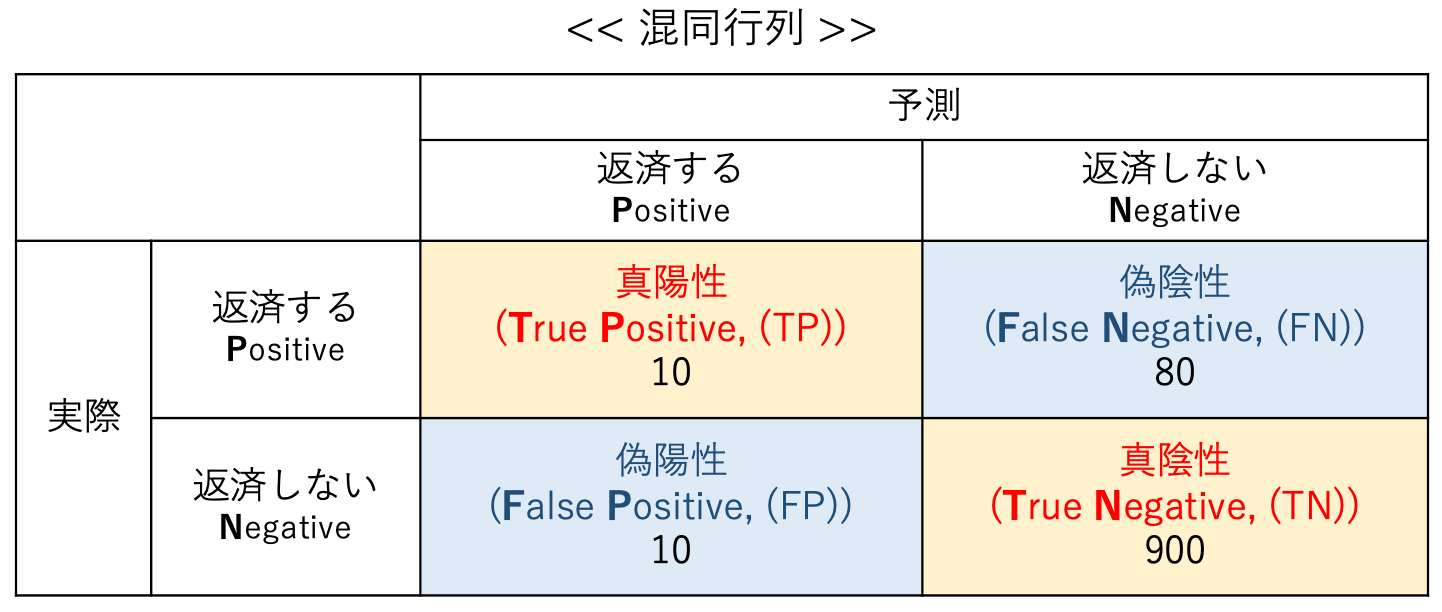と、上の図をみると思いますが、サッパリわからないというのが正直なところです。これを丸暗記というのも良いと思いますが、意味を理解しないと全く使えないので意味を理解していきましょう。

真陽性(True Positive：TP)
「融資を返済する」と予測したうち、ちゃんと「融資を返済したと判定できた」件数です。

真陰性(True Negative：TN)
「融資をしない」と予測したうち、ちゃんと「融資をしないと判定できた」件数です。

偽陽性(False Positive：FP)
ネガティブに分類すべきものを間違ってポジティブに分類してしまった件数を指します。つまり、「返済しない」はずなのに、「返済する」と判定してしまった件数。

偽陰性(False　Negative：FN)
ポジティブに分類すべきアイテムを誤ってネガティブに分類した件数を指します。
「返済する」に分類すべき人を「返済しない」に誤って分類した件数を指します。

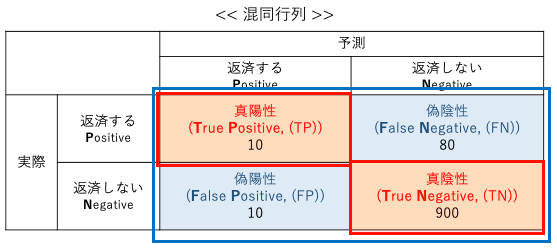
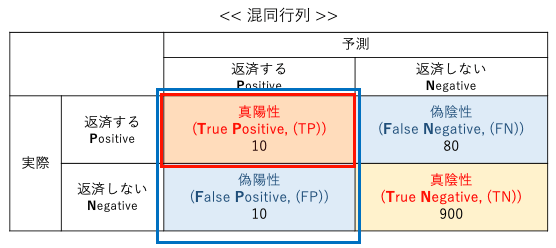
上図を例としますと、1000個のデータがあり、実際に融資を返済した人（TP+FN）が90人、返済しない人(FP+TN)が910人となります。
判定結果は、黄色い部分（TP+TN）の910人のデータは正解なので、一見90%以上の正確な予測結果に見えるのですが、実は・・・、実際に融資返済しない人（FN）が見過ごされているということがわかる。これはいいのか？わるいのか？はビジネスの課題にもなるのですが、そういうことです。

分類結果を検証する4つの手段

分類結果を検証には「正解率：accuracy」「適合率：precision」「再現率：recall」「F値」4つの手段があります。

正解率 (Accuracy)
全データのうち、実際にPositiveなデータをPositive予測し、NegativeなデータをNegativeと予測できた割合

$$正解率 (Accuracy) = \frac{TP + TN}{TP + TN + FP+ FN}$$

適合率 (Precision)
全データのうち、実際にPositiveなデータをPositive予測し、NegativeなデータをNegativeと予測できた割合

$$適合率 (Precision) = \frac{TP}{TP + FP}$$

再現率 (Recall)
全データのうち、実際にPositiveなデータをPositive予測し、NegativeなデータをNegativeと予測できた割合

$$再現率(Recall) = \frac{TP}{TP + FN}$$

再現率と適合率が高ければ高いほど、そのモデル性能は高いのですが、再現率と適合率の両者はトレードオフの関係になっています。そこで、双方を共に追求する際の指標として、両者の調和平均を意味するF値が参照されることもあります。

F値 (F-measure)
適合率と再現率の調和平均になります。F値が高いほど、バランスが良いモデルといえます。
$$F値(F-measure) = 2 \times \frac{適合率 \times 再現率}{適合率 + 再現率}$$

特異率(Specificity)
特異度（specificity）は、陰性のデータを正しく陰性と予測した割合でる。True negative rate (TNR) ともいいます。特異度の計算には、陽性データの予測結果が含まれないため、全てのデータを陰性と判定すれば（FP=0）、特異度を 100% にすることができます。
$$特異率(TNR) = \frac{FP}{FP + TN}$$

混同行列(Confusion Matrix)をPythonで確認する

sckit-learnをつかうとサクッとできてしまうので実際に動かしてみます。

from sklearn.metrics import confusion_matrix

y_true = [0, 0, 0, 0, 1, 1, 1, 0, 1, 0]
y_pred = [0, 0, 0, 0, 1, 1, 1, 1, 0, 1]
confusion_matrix(y_true, y_pred)

ndarrayで返されています。confusion_matrix()はカウントした値を行列に返しただけで、行列のどの要素がtp, fn, fp, tnなのかはまだ決まっていないです。

tp, fn, fp, tnを設定します。

tp, fn, fp, tn = confusion_matrix(y_true, y_pred).ravel()
(tp, fn, fp, tn)

(tp:4, fn:2, fp:1, tn:3)となりました。

sklearnのモジュールを利用して求めていきます。

# 正解率
from sklearn.metrics import accuracy_score
print('正解率：', accuracy_score(y_true, y_pred))

# 適合率
from sklearn.metrics import precision_score
print('適合率：', precision_score(y_true, y_pred))

# 再現率
from sklearn.metrics import recall_score
print('再現率：', recall_score(y_true, y_pred))

# F値
from sklearn.metrics import f1_score
print('F値：', f1_score(y_true, y_pred))

計算式を記述しなくともサクッと計算してくれます。非常に便利です。サンプルデータセットを利用して、もう少し細かくチェックしてみましょう。

乳がんデータセットで混同行列を確認する

チュートリアル的に乳がんデータセット「load_breast_cancer」で混同行列を確認していきましょう。必要なモジュールを読み込んでいきます。

解析は「ロジスティック回帰：LogisticRegression」を利用していきます。一連の処理を行うために「pipeline」を構築します。今回は、標準化（StandardScaler）、主成分分析（PCA）です。必ずこのセットというものはありませんので好みで設定してください。
confusion_matrixやaccuracy_score〜部分も先に紹介しているので割愛します。
roc_curve、aucは後述します。

# warningsを非表示にする
import warnings
warnings.filterwarnings('ignore')

import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
# pipelineに組み込む
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
#混合行列+可視化
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt

dataset = load_breast_cancer()

#説明変数と目的変数を分ける
X = pd.DataFrame(dataset.data, columns=dataset.feature_names)
y = pd.Series(dataset.target, name='y')

# 特徴量の確認
print(X.shape)
print(y.shape)

shapeにより、データ数569個、特徴量30個ということがわかりました。

from IPython.core.display import display
display(X.join(y).head())

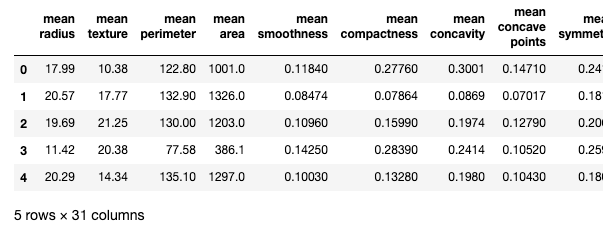
データの中身を確認すると上図のようになっています。

予測モデルを構築していきます。

# holdout
X_train,X_test,y_train,y_test=train_test_split(X, y, test_size=0.3, random_state=0)

# 訓練データの確認
print('X_train：',X_train.shape)
print('y_train：',y_train.shape)
# テストデータの確認
print('X_test：',X_test.shape)
print('y_test：',y_test.shape)

trainに398個、testに171個と別れました。

train_test_splitで分割します。test_size=0.3は7:3で訓練用データと検証用データを分けるという意味です。大概がこの割合だと思います。random_state=0の「0」はエンジニアによって「1」であったり、「123」であったりします。乱数を制御するパラメータです。チームで検証するときには、同じ値に設定することを推奨します。でないと毎回データにばらつきが生まれます。

訓練データと検証データに分けることができたので、予測モデルの構築を行います。今回は、Pipelineを使い、「標準化」「PCA」「ロジスティック回帰」を行います。

pipe_line = Pipeline([("scl", StandardScaler()),
              ("pca", PCA(n_components=2)),
              ("est", LogisticRegression())
             ])

pipe_line.fit(X_train, y_train)

モデルが構築できたので、予測結果をだします。
そして、混同行列により評価指標を持ちていきます。

# 予測値の算出
y_pred = pipe_line.predict(X_test)

# confusion matrixの作成
labels=[1,0]
cm = confusion_matrix(y_true=y_test, y_pred=y_pred, labels=labels)
print(cm)

print(y_test.value_counts())
print(pd.Series(y_pred).value_counts())

labels=labelsをしているていますが、これは指定しない場合、クラス「0」「1」の順番でソートされてしまうため、意図的に引数labelsをしてしています。参考に下のコードをご確認ください。

cm2 = confusion_matrix(y_true=y_test, y_pred=y_pred,)
print(cm2)

混同行列を可視化するためにヒートマップを利用します。

fig, ax = plt.subplots(figsize=(3,3))

ax.matshow(cm, cmap=plt.cm.Blues, alpha=0.7)
for i in range(cm.shape[1]):
    for k in range(cm.shape[0]):
        ax.text(x=k, y=i, s=cm[i, k], va='center', ha='center')
        
ax.set_xticklabels([""] + labels)
ax.set_yticklabels([""] + labels)
plt.xlabel("Predicted Class")
plt.ylabel("Actual Class")
plt.tight_layout()
plt.show()

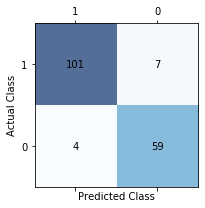ビジネスで提案資料にいれるとわかりやすいですね。正直、これくらいPPTの機能で十分作れるのでそんなに重きをおかなくて良いと思います。

評価指標を用いた結果を確認してみましょう。
正解率、適合率、再現率、F値です。

acc = accuracy_score(y_test, y_pred)
print(f"正解率(accuracy) : {acc*100:.2f}%")

pre = precision_score(y_test, y_pred)
print(f"適合率(precision) : {pre*100:.2f}%")

rec=recall_score(y_test, y_pred)
print(f"再現率(recall):{rec*100:.2f}%")

f1=f1_score(y_test, y_pred)
print(f"F1スコア:{f1*100:.2f}%") #F1 = 2 * (precision * recall) / (precision + recall)

sklearnを使うと非常に簡単に計算ができます。どの評価指標を使うかはビジネス課題に合わせて使ってください。

最後に、ROC曲線と、AUCスコアです。
False Positive Rate（偽陽性率）を横軸にTrue Positive Rate（真陽性率）を縦軸に置いてプロットしたものがROC曲線です。AUCは指標の名前通りROC 曲線下の面積となります。この面積の範囲が0〜1となり、ランダムが0.5です。曲線で判断するとすれば、１に近くなればなるほど精度が良いということになります。

#AUCスコア
Y_score = pipe_line.predict_proba(X_test)# 検証データがクラス1に属する確率を出す
Y_score = Y_score[:,1]

#print(Y_score)
fpr, tpr, thresholds = roc_curve(y_true=y_test, y_score=Y_score)

print('AUCスコア %0.3f' % auc(fpr, tpr))
plt.plot(fpr, tpr, label='roc curve (area = %0.3f)' % auc(fpr, tpr))
plt.legend()
plt.xlabel('false positive rate')
plt.ylabel('true positive rate')
plt.show()

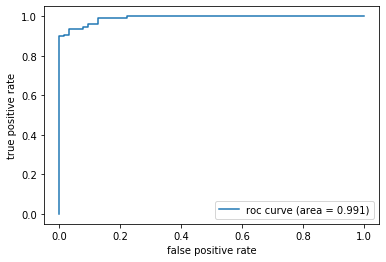
曲線をみると早い段階で「1」に近づいています。非常に良いモデルができていると考えることができます。

ただ、チュートリアルなので、綺麗なテーブルデータです。実務ではかなり汚いデータ、荒れているデータが多いので、しっかりと前処理を行い、使えるデータに仕上げてから分析することをおすすめします。というか必ず前処理やってからです。

最後に

混同行列(Confusion Matrix)のプログラムは多数ネットに落ちているので、コード自体は難しくないです。しかし、ビジネス課題にはめこむと「あれ？どっちだったけ？」となってしまうところがまだまだあるのでしっかり理解できるまで、資料をデスクトップにでも貼り付けておこうかと思います。目的に応じて自信を持って解答できるレベルになれるよう頑張ります。

多クラス分類の混同行列は複雑ということなので、また改めてまとめていきます。

---

なりたい自分になれる
スキルアップならUdemy

私も利用し、高収入エンジニアになったのよ。未経験から機械学習、データサイエンティスト、アプリ開発エンジニアを目指せるコンテンツが多数あります。優秀な講師が多数！割引を利用すれば1,200円〜から動画購入可能です。！

高収入エンジニアになる >>