自然言語処理関連に携われば、120%ベクトルというキーワードを耳にします。文字をベクトル化し、その距離を計算してうんぬんカンヌンするというものです。中身としては、文書、文字列、集合等について類似度を計算しています。その集合同士の類似度を計算する際によく利用される3つの係数をご紹介します。
- Jaccard係数
- Dice係数
- Simpson係数
私の業務では、Jaccard係数がメインなので、Jaccard係数に重きを置き、その他2つの係数はサクッとした説明にします。
Jaccard係数
Jaccard係数は、ある集合Aと別の集合BについてのJaccard係数J(A,B)は，以下の式で定義されます。
$$J(A,B)=\frac{|A \cap B|}{|A \cup B|}$$
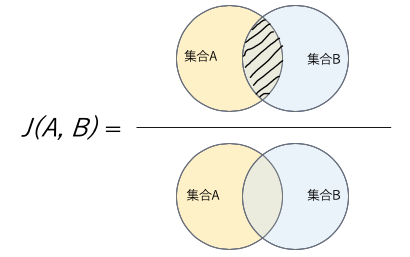
例えば、集合A = [1, 2, 3, 4]、 集合B = [3, 4, 8, 9] があったとします。\(|A \cap B|=2\)、\(|A \cup B|=6\) なので、Jaccard係数は \(\frac{2}{6}\)となります。
上記計算式からもわかる通り、2つの集合に含まれている要素のうち共通要素が占める割合を表しております。係数は0から1の間の値となることがわかります。Jaccard係数が大きいほど（１に近いほど）A と B は似ている(よく似ている)といえます。
Pythonで実装してみる
# Jaccard係数を計算
import numpy as np
import itertools
def jaccard(x,y):
# 積集合の要素数
intersection = len(set.intersection(set(x), set(y)))
# 和集合の要素数
union = len(set.union(set(x), set(y)))
# 分数表示で返す
return intersection / union
A = np.array([1, 2, 3, 4])
B = np.array([2, 3, 5, 7])
C = np.array([2, 4, 6])
tmp = [A, B, C]
### すべてのリストの組合せ作成
tmp2 = list(itertools.combinations(tmp, 2))
###すべての組合せにjaccard適用
for i in tmp2:
print(i[0],"&",i[1],":",jaccard(i[0], i[1]))
[1 2 3 4] & [2 4 6] : 0.4
[2 3 5 7] & [2 4 6] : 0.16666666666666666
他の求め方
def jaccard(data1, data2):
items = 0
for item in data1:
if item in data2:
items += 1
return items / (len(data1) + len(data2) - items)
data1 = ["リンゴ","ブドウ","イチゴ","パイン","キウイ","メロン"]
data2 =["メロン","イチゴ","リンゴ","パインアップル"]
jaccard(data1, data2)
Dice係数
Jaccard係数の定義式の分母はAにもBにも含まれている要素の数でしたが、これを「Aの要素数とBの要素数の共通要素数の割合平均」に変えるとDice係数となります。Dice係数が大きいほど2つの集合の類似度は高い(よく似ている)といえます。
ある集合Aと別の集合BについてのDice係数DSC(A,B)は，以下の式で定義されます。
$$DSC(A,B)=\frac{2|A \cap B|}{|A|+|B|}$$
例えば、集合A = [1, 2, 3, 4]、 集合B = [3, 4, 8, 9] があったとします。
\(|A| = 4 \)、\(|B| = 4\)、\(|A \cap B|=2\)なので、Dice係数は \(\frac{2\times 2}{4+4}=\frac{4}{8}\)となります。
Simpson係数
Jaccard係数の定義式の分母はAにもBにも含まれている要素の数でしたが、これを「Aの要素数とBの要素数のうちの小さい方」に変えるとSimpson係数になります。Simpson係数が大きいほど2つの集合の類似度は高い(よく似ている)といえます。
$$overlap(A,B)=\frac{|A \cap B|}{\min\{|A|,|B|\}}$$
例えば、集合A = [1, 2, 3, 4]、 集合B = [3, 4, 8, 9] があったとします。
\(|A| = 4 \)、\(|B| = 4\)、\(|A \cap B|=2\)なので、Simpson係数は \(\frac{2}{4}=\frac{2}{4}\)となります。
最後に
集合の類似度ということで「Jaccard係数」「Dice係数」「Simpson係数」を紹介しました。3つの係数にはある性質があります。
- Jaccard係数、Dice係数、Simpson係数は、いずれも 0 以上 1 以下
- AとBで共通部分を持たない時、3つの係数は全て０になります。逆に全て共通であれば係数は1になる
Dice係数、Simpson係数の実装はまたの機会にアップしたいと思います。
Jaccard係数で私が参考にさせてもらった資料はこちらです。
参考：
- ハイパーメディアのJaccard係数に着目した定義文拡張による語義曖昧性解消
- Jaccard係数の計算式（１）、（２）
- pythonでJaccard係数を実装
- 【技術解説】集合の類似度(Jaccard係数，Dice係数，Simpson係数)
なりたい自分になれる
スキルアップならUdemy
私も利用し、高収入エンジニアになったのよ。未経験から機械学習、データサイエンティスト、アプリ開発エンジニアを目指せるコンテンツが多数あります。優秀な講師が多数！割引を利用すれば1,200円〜から動画購入可能です。！
