今回は、自然言語処理の基礎「TF-IDF」を自分なりにまとめたので紹介します。
目次
TF-IDFとは
TF-IDF(Term Frequency – Inverse Document Frequencyの略)は、文書中に含まれる単語の重要度を評価する手法の1つです。ある文書を特徴づける重要な単語を抽出したいときに有効な手法で、TF-IDFはTFとIDFの2つの指標を掛け合わせた値になります。
- TF(Term Frequency): ある文書における単語の出現頻度
- IDF(Inverse Document Frequency): 逆文書頻度
TF(Term Frequency)
文書内でのある単語の出現頻度です。いくつかの文書があり、ある文書中に頻度が多ければ多い程、その単語は重要である可能性が高いと評価するものです。
計算式
$$TF(t_i,d_j)=\frac{文書d_j内の単語t_iの出現回数}{文書d_jのすべての単語の出現回数の和}=\frac{f(t_i,d_j)}{\sum_{t_k\in d_j}f(t_k,d_j)}$$
簡単に考えると「単語数が多ければその文書をよく表している」と考えてしまうかもしれないですが、実はそうでもないです。例えば、「デザイナーの仕事」と「エンジニアの仕事」では「Web」という単語が頻繁にみられるかもしれない。しかし、「Web」という単語ではそれぞれの文書の特徴を捉えているとは考えにくいからです。
そこで考えるべきことが「その単語(例:Web)が他の文書で含まれていない」を表すことです。その値をIDF値といいます。
IDF(Inverse Document Frequency)
それぞれの単語がいくつか(いくつ)の文書内で共通して使われているかを表します。逆に考えるのであれば、「ある単語が他の文書で含まれていない」と考えることもできます。単語がレア頻出であればあるほど、高い値になります。
計算式
$$IDF(t_i)=\log{}\left(\frac{総文書数}{単語t_iが出現する文書数}+1\right)=\log{}\left(\frac{N}{df(t_i)}+1\right)$$
1が足されているのは、文書全体に登場する単語が0の場合、計算できないため(0除算になってしまうため)です。
TF-IDF
TF-IDF値は、TF値とIDFの値を掛け合わせた値です。
ある文書内での出現回数は多い(TDF)と他の文書には出現していない単語(IDF)を計算することで、単語毎の重要度を算出することが可能になります。
英文を例にとると、カウントベースでaやthisは頻繁に登場するはずです。文書内に頻繁に出力される単語なので大きな影響を与えてしまうかもしれません。しかし、TF-IDFを使った場合は、文書には出現していない単語(IDF)も考慮されています。されるため、ただ多く登場すれば重要になるという単純な部分を少しケアしていることになります。
公式
$$tfidf(t_i,d_j)=tf(t_i,d_j)・idf(t_i)
=\frac{f(t_i,d_j)}{\sum_{t_k\in d_j}f(t_k,d_j)}・\log{}\left(\frac{N}{df(t_i)}+1\right)$$
Pythonで実装してみる
Pythonで実装してみます。
以下のような2つの文章があったとします。
- A:リンゴとみかんとみかんとバナナ
- B:バナナとイチゴとイチゴとぶどうとみかん
本来であれば形態素解析を行い、名詞を抽出してから確認しますが、今回は飛ばします。
各名詞をリストに格納し、重複チェックをかけ、ソートしておきます。
from math import log
import pandas as pd
docs = [
['リンゴ', 'みかん', 'みかん', 'バナナ'],
['バナナ', 'イチゴ', 'イチゴ', 'ぶどう', 'みかん']
]
words = list(set(w for doc in docs for w in doc))
words.sort()
words
関数を作成します。
N = len(docs)
def tf(t, d):
return d.count(t)/len(d)
def idf(t):
df = 0
for doc in docs:
df += t in doc
return log(N/df)+1
def tfidf(t, d):
return tf(t,d)* idf(t)
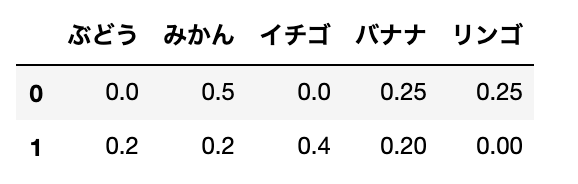
まず、TFの値を計算します。
# TF
result = []
for i in range(N):
result.append([])
d = docs[i]
for j in range(len(words)):
t = words[j]
result[-1].append(tf(t,d))
tf_ = pd.DataFrame(result, columns=words)
tf_
IDFの値を計算します。
# IDF
result = []
for j in range(len(words)):
t = words[j]
result.append(idf(t))
idf_ = pd.DataFrame(result, index=words, columns=["IDF"])
idf_

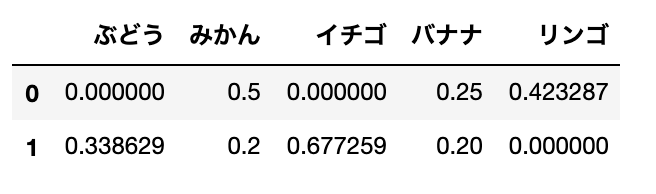
TFとIDFがもとまったので、TF-IDFを計算します。
# TF-IDF
result = []
for i in range(N):
result.append([])
d = docs[i]
for j in range(len(words)):
t = words[j]
result[-1].append(tfidf(t,d))
tfidf_ = pd.DataFrame(result, columns=words)
tfidf_
今回のデータは以下の2つです。
- A:リンゴとみかんとみかんとバナナ
- B:バナナとイチゴとイチゴとぶどうとみかん
2つの文書に登場している「みかん」「バナナ」は値が小さいです。逆に、片方しか登場していない「イチゴ」は値が高いことがわかります。
TF-IDFの欠点
TF-IDFの計算では、文書に含まれる単語数が多いほどTF値が値が小さく、単語数が少ないほどTF値が大きくなる。理由は、分母に「全ての単語の出現回数の和」をとっているからです。つまり、複数の文書から重要度の高い単語を抽出して絶対評価でTF-IDFで比較する場合、文書ごとの単語数の差による影響が大きく出てしまうということです。極端に説明するとすれば、文字数の多い(文面が長い)文書とそうでない文書では影響度合いが違うということです。
絶対的な評価ではなく、相対的に評価するOkapi BM25という手法もあります。
Okapi BM25は、情報検索における順位付けの手法である。検索エンジンがクエリとの関連性に応じて、文書を順位付けするのに用いられる。1970年代から1980年代にかけて、スティーブン・ロバートソンやカレン・スパーク・ジョーンズらが確率適合モデル(英語版)に基づいて開発した。BM25の “BM” は、 “Best Matching” の略である。
wikipedia:https://ja.wikipedia.org/wiki/Okapi_BM25
Okapi BM25については、またの機会に自分なりにまとめていたいと思います。
最後に
自然言語処理の基礎TF-IDFについて簡単ではありますが、まとめて見ました。
実際に実務で使うとなると以下のライブラリなどを利用します。
- tfidfvectorizer(sklearn)
- CountVectorizer(sklearn)
- models.tfidfmodel(gensim)
次回は、tfidfvectorizerなどのライブラリを利用し、解析に取り組んでみます。
参考:
【初学者向け】TFIDFについて簡単にまとめてみた
【技術解説】単語の重要度を測る?TF-IDFとOkapi BM25の計算方法とは
自然言語処理の基礎であるTF-IDFの計算方法とPythonによる実装方法を解説